
![]() 添加好友 领取资料
添加好友 领取资料
通过对近年来国家公务员考试和各地市公务员考试行政职业能力测验真题的分析,不难发现,计数性质的试题经常出现在数量关系部分的数学运算中。而此类试题在运算的过程中又因为容易遗露某个条件而漏计或重复计数出现错误。
例题:
某市对52种建筑防水卷材产品进行质量抽检,其中有8种产品的低温柔度不合格,10种产品的可溶物含量不达标,9种产品的接缝剪切性能不合格,同时两项不合格的有7种,有1种产品这三项都不合格。则三项全部合格的建筑防水卷材产品有多少种?
A.34 B.35 C.36 D.37
为便于解决此类计数问题,不妨先让我们引入小学奥数中经常用到的一个原理,即容斥原理:
在计数时,必须注意无一重复,无一遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先容纳(计算)进去,然后再把计数时重复计算的数目排斥出去(减去),使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
容斥原理中经常用到的有如下两个公式:
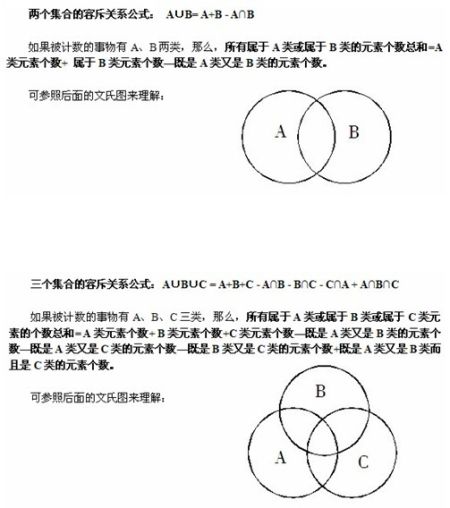
运用上述两个公式需要注意以下情况:
这两个公式分别主要针对两种情况:第一个公式是针对涉及到计算两类事物的个数,第二个公式是针对涉及到三类事物的个数。
在理清了容斥原理之后,再来计算前面所提到的例题就会发现,运用容斥原理解决此类问题就会方便很多。
一、运用容斥原理公式来解题
题干中所要寻找的是三项全部合格的建筑防水卷材产品有多少种,而这道题已经给出了这三项建筑防水卷材产品总共有52种,所以,只要求得至少有一项不达标的产品的种数,就可以计算出三项全部合格(达标)的产品种数。而不合格的产品涉及到三种情况,所以运用三个集合的容斥关系公式成了解决此题的不二选择。
假设B是低温柔度不合格产品的集合,A是可溶物含量不达标的产品集合,C属于接缝剪切性能不合格的产品集合,则:

当然,此题还有一种相对较为容易理解的算法,即用文氏图法。
二、借助文氏图来计算
如下图所示,I是所有建筑防水卷材产品的集合,A是可溶物含量不达标的产品集合,B是低温柔度不合格产品的集合,C属于接缝剪切性能不合格的产品集合,图中的数字即是相应集合中元素的个数。
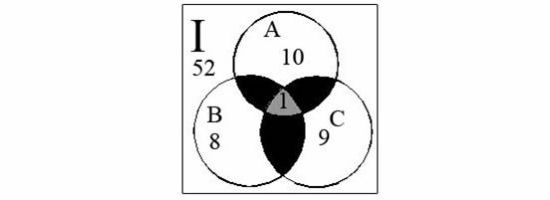
图中黑色部是同时两项不格的产品集合,灰色部是这三项都不合格的产品集合。计算至少有一项不达标的产品的种数时候,黑色部分重复计算了一次,灰色部分复计算了两次,所以,至少有一项不达标的产品的种数有10+8+9-7×1-1×2=18(种)进而可求出三项全部合格的建筑防水卷材产品有(52-18)种,即34种。
考生在学习本文时,要注意以下两点:
1、文氏图表示的都是相应的集合,而本篇文稿所提到的要解决的问题则是计算集合内事物个数的问题。
2、一般情况下,较为容易的采用容斥原理公式来计算,较为复杂则需借助文氏图。
所谓具体问题具体分析,这两种方法具体如何运用,考生还要针对不同题型灵活把握。
行测更多解题思路和解题技巧,可参看华图教育国考解析
本文链接:http://chifeng.huatu.com/2012/0229/299945.html
(编辑:张老师)

微信公众号

贴心微信客服


















































